堆本质是一棵二叉树,其中所有的元素都可以按全序语义进行比较。
用堆来进行存储需要符合以下规则:
-
元素可比较性:数据集中的元素可以进行比较。
-
节点最大/最小性:每个节点的元素必须大于或小于该节点的孩子节点的元素。
-
堆是一棵完全二叉树。
分类
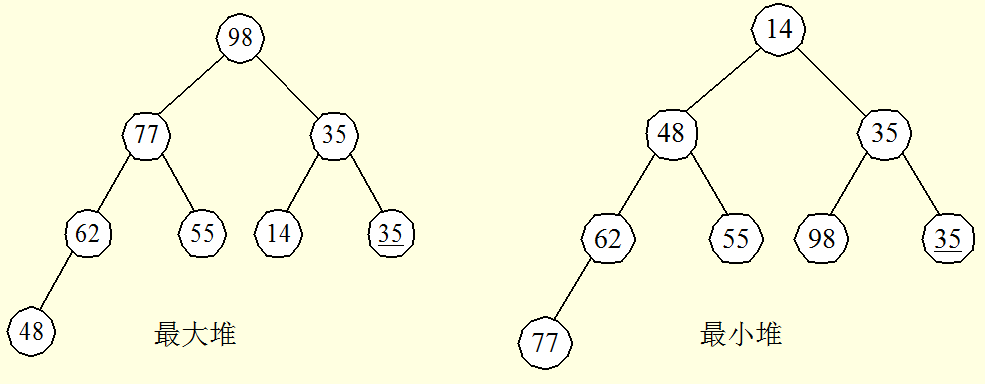
堆有两种:最大堆和最小堆。
最小堆中每个节点的优先级小于或者等于它的子节点;最大堆则相反,每个节点的优先级都大于或者等于它的子节点。
存储
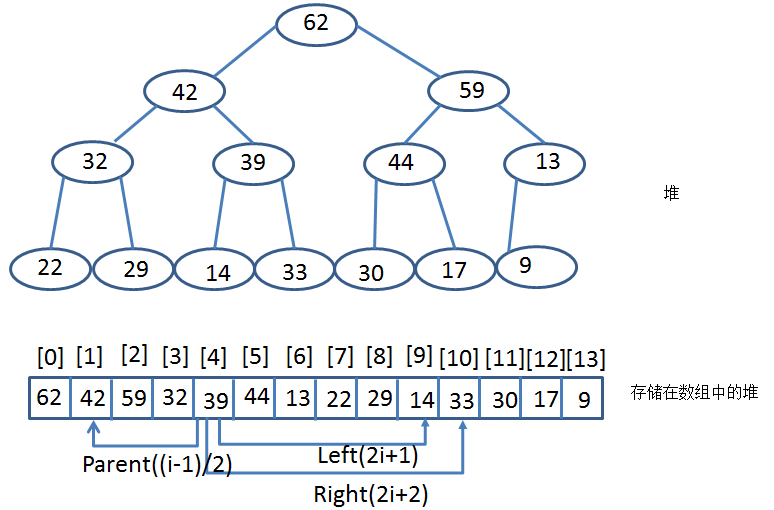
堆的存储是通过数组实现:
-
根节点位置:根节点的数据总是在数组的位置[0]
-
节点的父节点位置:假设一个非根节点的数据在数组中的位置 [i],那么它的父节点总是在位置 [(i-1)/2]
-
节点的孩子节点位置:假设一个节点的数据在数组中的位置为 [i],那么它的孩子(如果有)总是在下面的这两个位置:左孩子在 [2i+1],右孩子在[2i+2]
操作
在堆中主要是插入和删除节点的操作,这两种操作无论是哪一种,完成之后都还是一个堆,操作时要进行堆的调整,使其是个新堆。
插入节点
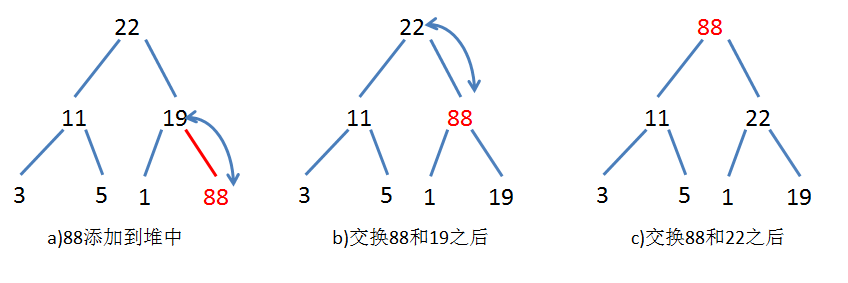
插入的思路是这样的:当插入一个元素时,先将这个元素插入到队列尾,然后将这个新插入的元素和它的父节点进行优先权的比较,如果比父节点的优先权要大,则和父节点呼唤位置,然后再和新的父节比较,直到比新的父节点优先权小为止。
删除节点
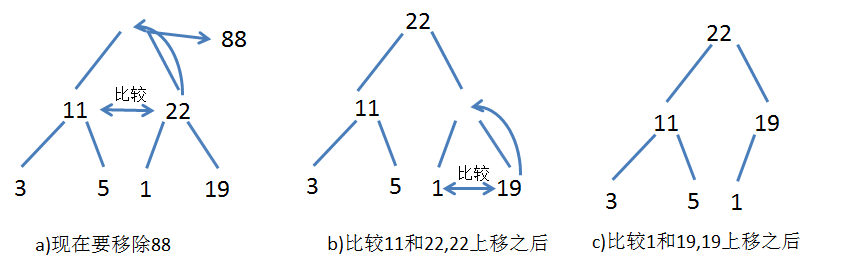
从堆中删除优先权最大的元素的思路是将队列尾的元素值赋给根节点,队列为赋 值为 null。然后检查新的根节点的元素优先权是否比左右子节点的元素的优先权大,如果比左右子节点的元素的优先权小,就交换位置,重复这个过程,直到秩序正常。
应用
堆应用比较多的一个用处就是堆排序,对于一个数组进行堆化之后,第一个数组是最大的值,然后交换第一个数和最后一个数,这样最大的数就落在了最后一个数组的位置。缩小数组,重复之前的步骤,最后就得到了一个排序好的数组。
参考
https://blog.csdn.net/tuke_tuke/article/details/50357939
https://segmentfault.com/a/1190000018693247