Jacky's Blog

数据结构之散列表

2020/08/28

数据结构中的线性表和数等，记录在结构中的位置是不固定的，查找元素时需经过一系列和关键字的比较。而在哈希表中，元素和位置存在某种对应关系，查找元素时可根据关键字一次存取便可取得元素。

定义

根据散列函数（即哈希函数）H(key)和处理冲突的方法将一组关键字映像到一个有限的连续的地址集上，并以关键字在地址集中的“象”作为记录在表中的存储位置，这种表便称为散列表（即哈希表），这一映像过程称为散列造表或散列，所得的的存储位置称散列地址。

若 key1≠key2，而 f(key1)=f(key2)，这种现象称为冲突（即碰撞）。具有相同函数值的关键字对该散列函数来说称为同义词，即 key1 和 key2 对于散列函数 f(key) 来说是同义词。

若对于关键字集合中的任一关键字，经散列函数映像到地址集合中任何一个地址的概率是相等的，则称为此类散列函数为均匀散列函数。

散列函数性质

所有散列函数都有如下基本特性：

  1. 如果两个散列值不相同，则这两个散列值的原始输入也是不同的。

  2. 如果两个散列值相同，则两个输入值有可能相同，有可能不相同，相同的概率很大。

也即散列值对应输入值的关系是一对多，一个散列值可以对应多个输入值，而输入值对应散列值的关系是一对一，一个输入值经过散列函数只能得到一个散列值。

散列函数构造方法

好的散列函数参考原则：

  1. 计算简单。散列函数的计算时间不应该超过其他查找技术与关键字比较的时间。

  2. 散列地址均匀分布。地址均匀分布，可以保证存储空间的有效利用，减少为处理冲突而耗费的时间。

常见散列函数构造方法如下：

直接定址法

取关键字或关键字的某个线性函数值为哈希地址，即 H(key)=key 或 H(key)=a*key+b。由于直接定址法所得地址集合和关键字集合大小相同，因此对于不同的关键字不会发生冲突，但实际中使用这种哈希函数的情况很少。直接定址法适用于事先知道关键字的分布情况，查找表较小且连续的情况。

例：制作 0~100 岁的人口数字统计表，可将关键字 0~100 分别对应存放于 0~100 的连续地址中，此时 H(key)=key。

数字分析法

分析关键字中的数字，找出差异较大的部分作为哈希函数的输入值。数字分析法适用于事先知道关键字的分布情况，关键字较长且若干位分布较均匀的情况。

例：根据某单位员工的手机号码制作散列表，可取手机号码的后四位作为散列表的输入。

平方取中法

取关键字平方后的中间几位数字作为哈希函数的输入值。一个数的平方中间几位与每位数字都有关，当数字分析法不合适时，可考虑使用此方法。平方取中法适用于不知道关键字的分布且位数又不是很大的情况。

例：1) 关键字 1234 的平方是 1522756，取中间三位就是 227。2) 关键字 4321 平方是 18671041，取中间三位为 671 或 710。

折叠法

将关键字从左到右分割成位数相等的几部（最后一部分位数允许短些），然后将这几部分叠加求和，并按散列表表长，取后几位作为散列地址。折叠法事先不需要知道关键的分布，适用于关键字位数较多的情况。

例：散列表表长为 0~999，地址位数为 3 位，我们将关键字 9876543210 分为四组，987|654|321|0，然后这几部分求和 987+654+321+0=1962，取后 3 位 962 即为散列地址。

除留余数法

取关键字或关键字折叠、平方取中后对某个数 p 取模，对于散列表表长为 m 的散列函数公式为：H(key)=key mod p(p<=m)。

除留余数法最重要的就是 p 的选择，p 选择的好坏直接影响冲突的个数。前辈们的经验，通常 p 为小于等于表长 m（最好接近 m）的最小质数或不包含小雨 20 质因子的和数。

随机数法

H(key)=random(key)。

处理冲突的方法

再好的散列函数也只能尽可能减少冲突的发生，却不能完全避免冲突的发生。因此，在构造散列表时必须考虑冲突发生后的处理方法。

常见处理冲突的方法如下：

开放定址法

一旦发生冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。

  1. 线性探测再散列：f(key)=(f(key)+di) mod m(di=1,2,3…m-1)。当发生冲突时，向下逐个查找，直到找到一个空地址。缺点：关键字堆积严重，效率较低。

  2. 二次探测再散列：f(key)=(f(key)+di) mod m(di=1²,-1²,2²,-2²,…,q²,-q²,q<=m/2)。发生冲突时，向两侧双向查找，可避免关键字聚集在某一块区域。

  3. 随机探测再散列：f(key)=(f(key)+di) mod m(di是一个随机数列)。di 是伪随机数，通过随即种子产生。

再散列函数法

事先准备多个散列函数，冲突发生时，就更换一个散列函数重新计算散列地址。fi(key)=RHi(key)(i=1,2,…k)

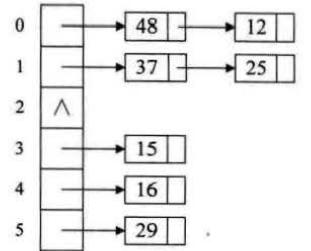
链地址法

将所有关键字为同义词的记录存储在一个单链表中。链地址法不会出现找不到地址的情况，同时，在查找时需要遍历单链表，带来了一定的性能损耗。

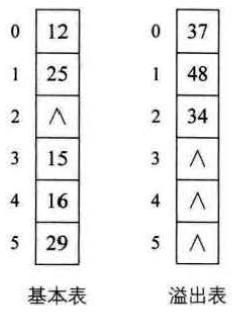
公共溢出区法

为所有的冲突的关键字建立一个公共的溢出区并保存。在查找时，对给定值通过散列函数计算出散列地址后，先与基本表相应位置进行比对，若相等，查找成功；若不想等，则到溢出表顺序查找对应记录。在冲突很少的情况下，公共溢出区法效率还是非常高的。

散列表的查找

散列表查找时，现根据散列函数将关键字转换成散列地址，再到对应的散列地址中取值，若值的标记与关键字相等，则查找成功；若不相等，则说明该关键字值存在冲突，根据相应处理冲突的方法进行相应的查找。

散列表的平均查找长度取决于以下因素：

  1. 散列表是否均匀。

  2. 处理冲突的方法。

  3. 散列表的装填因子（装填因子 a= 关键字个数/散列表长度）。

参考

https://www.cnblogs.com/hanganglin/articles/3737506.html

Post Directory