线性表局限于一个直接前驱和一个直接后继的关系,树也只能有一个直接前驱也就是父节点。当我们需要表示多对多的关系时,就需要用到图。
图的定义和基本术语
图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G 表示一个图,V 是图 G 中顶点的集合,E 是图 G 中边的集合。
边:两个顶点之间的连接。
路径:一个顶点到另一个顶点的通路。
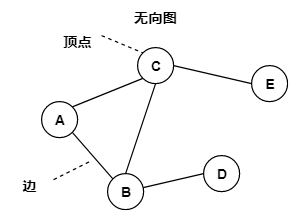
无向图(Undirected Graph):顶点之间的路径没有方向,比如 A-B,即可以是 A->B 也可以 B->A,下面的图就是一个无向图。
有向图(Directed Graph):顶点之间的路径有方向,比如 A-B,只能是 A->B,不能是 B->A,下面的图就是一个有向图。
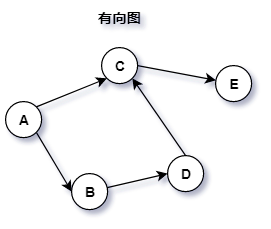
出度(Out-degree):一个顶点的出度为 x,是指有 x 条边以该顶点为起点,例如上面的有向图中,顶点 A 的出度是 2。
入度(In-degree):一个顶点的入度为 x,是指有 x 条边以该顶点为终点,例如上面的有向图中,顶点 C 的入度是 2。
出度、入度适用于有向图。
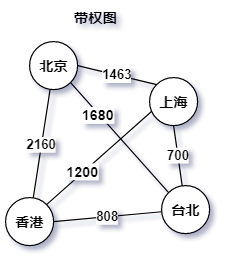
带权图(Weighted Graph):边带权值的图也叫网。
图的表示方式
邻接矩阵(Adjacency Matrix)
邻接矩阵是表示图形中顶点之间相邻关系的矩阵,通常采用一个存放顶点信息的一位数组和一个存放边信息的二维数组实现。
使用邻接矩阵实现的无向图如下:
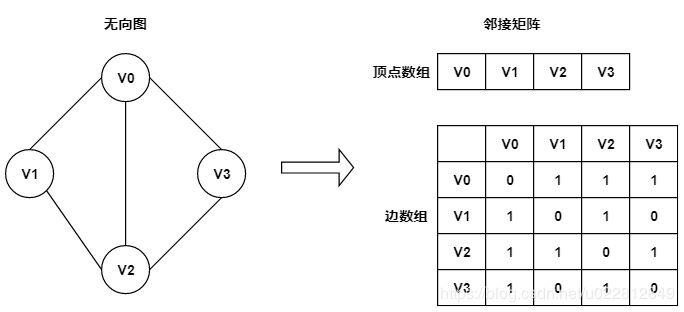
说明:
-
邻接矩阵中的1代表两个顶点之间直连,0 代表两个顶点之间不直连。
-
顶点V1与顶点 V0 和顶点 V2 直连,所以邻接矩阵的第二行第一列和第三列为 1。
使用邻接矩阵实现的有向图如下:
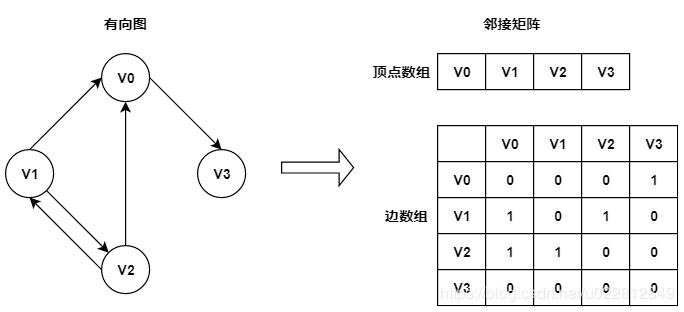
邻接矩阵比较适合稠密图,不然会比较浪费内存。
邻接表(Adjacency List)
邻接矩阵需要为每个顶点都分配 n 个边的空间,其实有很多边都是不存在,会造成空间的一定损失。
邻接表的实现只关心存在的边,不关心不存在的边。因此没有空间浪费,邻接表由数组+链表组成。
使用邻接表实现的无向图如下:
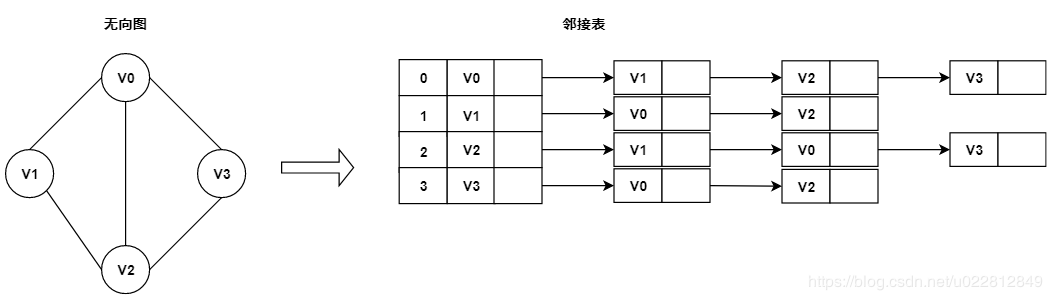
说明:
- 顶点 V1 与顶点 V0 和顶点 V2 直连,所以顶点 V1 对应的链表为 V0->V3。
使用邻接表实现的有向图如下:
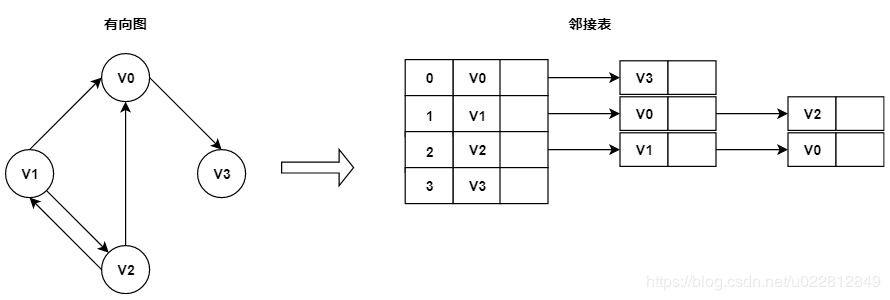
参考
https://www.jianshu.com/p/d9ca383e2bd8
https://blog.csdn.net/u022812849/article/details/107000563