树是由结点或顶点和边组成的(可能是非线性的)且不存在着任何环的一种数据结构。没有结点的树称为空(null 或 empty)树。一棵非空的树包括一个根结点,还(很可能)有多个附加结点,所有结点构成一个多级分层结构。
树的相关术语
-
节点的度:一个节点含有的子树的个数称为该节点的度。
-
叶节点或终端节点:度为 0 的节点称为叶节点。
-
非终端节点或分支节点:度不为 0 的节点。
-
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。
-
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点。
-
兄弟节点:具有相同父节点的节点互称为兄弟节点。
-
树的度:一棵树中,最大的节点的度称为树的度。
-
节点的层次:从根开始定义起,根为第 1 层,根的子节点为第 2 层,以此类推。
-
树的高度或深度:树中节点的最大层次。
-
堂兄弟节点:双亲在同一层的节点互为堂兄弟。
-
节点的祖先:从根到该节点所经分支上的所有节点。
-
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
-
森林:由 m(m>=0)棵互不相交的树的集合称为森林。
二叉树
二叉树是数据结构中一种重要的数据结构,也是树表家族最为基础的结构。
二叉树的定义:二叉树的每个结点至多只有二棵子树(不存在度大于 2 的结点),二叉树的子树有左右之分,次序不能颠倒。二叉树的第 i 层至多有 2i-1 个结点;深度为k的二叉树至多有 2k-1 个结点;对任何一棵二叉树 T,如果其终端结点数为 n0,度为 2 的结点数为 n2,则 n0=n2+1。
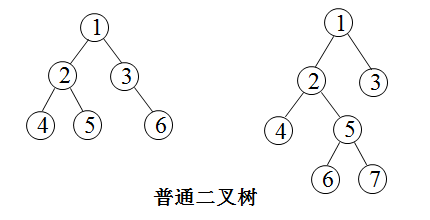
二叉树的遍历方法
中序遍历:即左-根-右遍历,对于给定的二叉树根,寻找其左子树;对于其左子树的根,再去寻找其左子树;递归遍历,直到寻找最左边的节点i,其必然为叶子,然后遍历i的父节点,再遍历i的兄弟节点。随着递归的逐渐出栈,最终完成遍历
先序遍历:即根-左-右遍历
后序遍历:即左-右-根遍历
满二叉树
一棵深度为 k 且有 2k-1(2 的 k 次幂减 1)个结点的二叉树称为满二叉树。
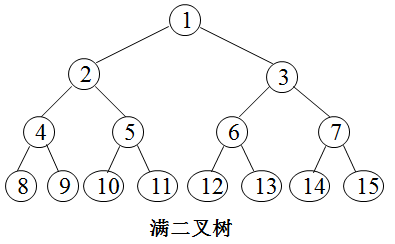
完全二叉树
深度为 k 的,有 n 个结点的二叉树,当且仅当其每一个结点都与深度为 k 的满二叉树中编号从 1 至 n 的结点一一对应时,称之为完全二叉树。
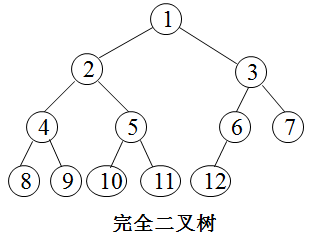
二叉排序树
二叉查找树定义:又称为是二叉排序树(Binary Sort Tree)或二叉搜索树。二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
-
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值。
-
若它的右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值。
-
它的左、右子树也分别为二叉排序树。
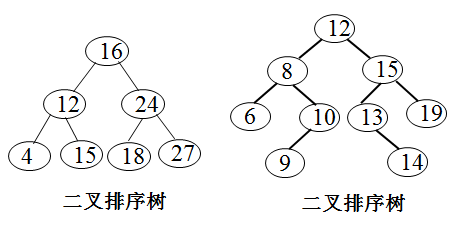
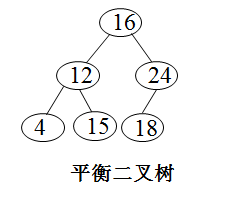
平衡二叉树
平衡二叉树(Balanced Binary Tree)又被称为 AVL 树。它或者是一棵空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过 1。(注:平衡二叉树应该是一棵二叉排序树)
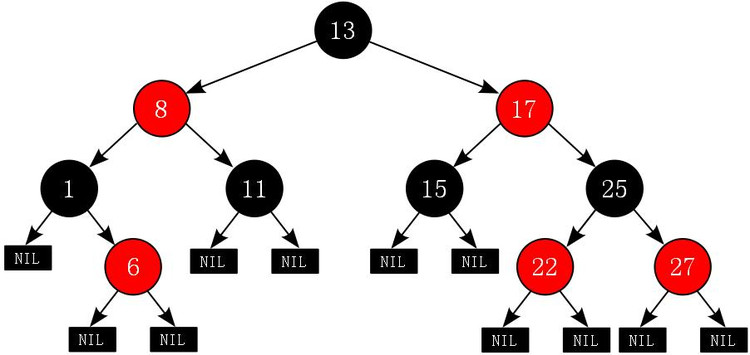
红黑树
红黑树,一种二叉查找树,但在每个结点上增加一个存储位表示结点的颜色,可以是 Red 或 Black。通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出 2 倍,因而是近似于平衡的。树中每个结点包含 5 个属性:color、key、left、right 和 p。如果一个结点没有子节点或父节点,则该结点相应的指针属性值为 NIL,我们可以把这些 NIL 视为指向二叉搜索树的叶节点(外部结点)的指针,而把带关键字的结点视为树的内部结点。
一棵红黑树是满足下面性质的二叉搜索树:
-
每个结点或是红色的,或是黑色的。
-
根结点是黑色的。
-
每个叶结点(叶结点即指树尾端 NIL 指针或 NULL 结点)是黑的。
-
如果一个结点是红色的,则它的两个子结点都是黑色的。
-
对每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。
红黑树虽然本质上是一棵二叉查找树,但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡,从而保证了红黑树的查找、插入、删除的时间复杂度最坏为 O(log n)。
B 树
B 树又称为 B- 树,是一种平衡的多路查找树。B- 树的阶是所有结点的孩子结点树的最大值。一棵 m 阶 B- 树,或为空树,或为满足下列特性的 m 叉树:
-
树中每个结点至多有 m 棵子树。
-
若根节点不是叶子节点,则至少有两棵子树。
-
除根之外的所有非终端结点至少有 [m/2](向上取整)棵子树。
-
所有的非终端结点中包含下列信息数据:(n,A0,K1,A1,K2,A2,…,Kn,An),其中,n 为结点中的关键字树,A 为指向子树根结点的指针,K 为关键字,且 Ai-1 所指子树中所有结点的关键字均小于 Ki,An 所指子树中所有结点的关键字均大于 Kn。
-
所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
下图为一棵 4 阶 B- 树:
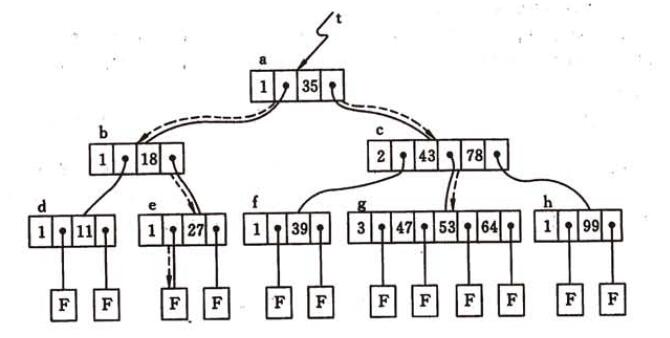
B+ 树
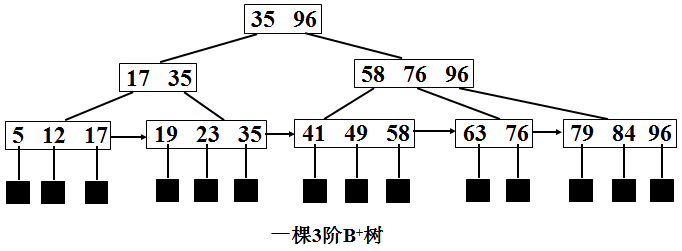
B+ 树是应文件系统所需而出的一种 B- 树的变型树。一棵 m 阶 B+ 树和 m 阶的 B- 树的差异在于:
-
有n棵子树的结点中含有 n 个关键字,每个关键字不保存数据,只用来索引,所有数据都保存在叶子节点。
-
所有的叶子结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
参考
https://www.jianshu.com/p/912357993486
https://blog.csdn.net/hero_myself/article/details/52080969