算法复杂度分为时间复杂度和空间复杂度。其作用:
-
时间复杂度是指执行这个算法所需要的计算时间。
-
空间复杂度是指执行这个算法所需要的内存空间。
时间和空间都是计算机资源的重要体现,而算法的复杂性就是体现在运行该算法时的计算机所需的资源多少。
算法复杂度
空间复杂度
一个程序的空间复杂度是指运行完一个程序所需内存的大小。利用程序的空间复杂度,可以对程序的运行所需要的内存多少有个预先估计。一个程序执行时除了需要存储空间和存储本身所使用的指令、常数、变量和输入数据外,还需要一些对数据进行操作的工作单元和存储一些为现实计算所需信息的辅助空间。程序执行时所需存储空间包括以下两部分。
-
固定部分:这部分空间的大小与输入/输出的数据的个数多少、数值无关。主要包括指令空间(即代码空间)、数据空间(常量、简单变量)等所占的空间。这部分属于静态空间。
-
可变空间:这部分空间的主要包括动态分配的空间,以及递归栈所需的空间等。这部分的空间大小与算法有关。
时间复杂度
关于时间频度: 一个算法执行所耗费的时间,从理论上是不能算出来的,必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试,只需知道哪个算法花费的时间多,哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为 T(n)。
在刚才提到的时间频度中,n 称为问题的规模,当 n 不断变化时,时间频度 T(n) 也会不断变化。但有时我们想知道它变化时呈现什么规律。为此,我们引入时间复杂度概念。记为 O(…),也称为大 O 表示法;
另外,时间频度不同,但时间复杂度可能相同。如:T(n)=n2+3n+4 与 T(n)=4n2+2n+1 它们的频度不同,但时间复杂度相同,都为 O(n2) //注意这里 n2 是 n 方的意思。
时间复杂度去估算算法优劣的时候注重的是算法的潜力,也就是在数据规模有压力的情况之下(最坏情况)算法的执行频度,什么意思呢?比如 2 个算法,在只有 100 条数据的时候,算法 a 比算法 b 快,但是在有 10000 条数据的时候算法 b 比算法 a 快,这时候我们认为算法 b 的时间复杂对更优。
时间复杂度与空间复杂度的取舍问题
就目前来说,除了在一些特殊情况下,我们都是更加注重时间复杂度,而不是空间复杂度。注意,这里我们强调了,除了一些特殊情况外,有些特殊情况下,空间复杂度可能会更加重要。
那么,究竟什么时候应该着重考虑时间复杂度,什么时候应该着重考虑空间复杂度呢?我们来看一个例子:
设想现在需要由你来完成一个程序设计,程序要求是这样的:要求输入年份,返回该年份是否是闰年。
一提到这个问题,我想如果你学习过任何一门语言,你可能都做过类似的题目。你可能思路已经非常清晰了,满百除四百,不满除以 4。
额,先不要急。我们来看看还能不能进一步提高性能,降低时间复杂度。也就是用空间复杂度来换取时间复杂度。比如,如果使用我们程序的用户,只会查看当前年份未来几年和过去几年的日历的话,我们完全可以使用一个比如:2100 个元素的数组,每个元素为 0 或 1,分别表示平年和闰年。这样当用户查询的时候,就不需要再进行复杂的逻辑判断,而只需要取出对应下标位置的元素即可。 反过来,如果我们的用户经常查询跨度上万年的日历信息(万年历),那么,我们肯定不能使用上面牺牲空间复杂度来换取时间复杂度的方案解决。因为如此巨大的空间消耗是我们损失不起的。
而,编程的精髓和美,并不在于一方的退让和妥协。而是在于如何在二者之间取一个平衡点,完成华丽变身。那么,对于我们这种程序应该如何权衡呢?
我想到的一种方案是:将与当前年份相近的几年存为固定数据,查询时只需要读取即可。而对于那些和当前年份相距较远的年份的数据,在用户请求查询时动态生成。
这样,既能在损失可接受空间的情况下,大幅度提高性能,又能保证空间的损失不至于太大而无法接受。我想当用户查询据今较远的数据时,有一些时间上的等待,也是可以接受的。
总结下这一段的核心思想: 不能简单的说时间复杂度就比空间复杂度重要,在特定场景下空间复杂度反而比时间复杂度重要,在程序中我们需要综合考虑让时间和空间的消耗达到一个平衡点,从上面平闰年计算的例子来看,我们可以缓存前后几年间的平润年,因为内存开销在可控范围内,至少是在现有条件下能够体验到的可接受范围,所以这几年的数据我们可以用增大空间消耗来减少时间的消耗,如果说要将一万年的所有平闰年数据都存上,那么即便是内存能撑得住也是得不偿失的,所以这时候我们用增大时间开销(网络请求,动态加载)去交换减少空间的开销(省去了万级数据的存储空间);所以综上,这就是个综合考量的问题。
如何计算一个算法的时间复杂度?
算这个时间复杂度实际上只需要遵循如下守则:
-
用常数 1 来取代运行时间中所有加法常数。
-
只要高阶项,不要低阶项。
-
不要高阶项系数。
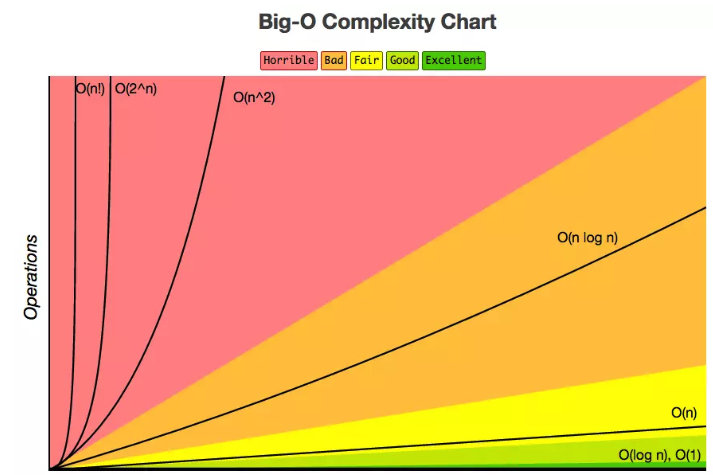
常见的时间复杂度
按增长量级递增排列,常见的时间复杂度有:
- O(1) — 常数阶
- O(N) — 线性阶
- O(log2N) — 对数阶
- O(nlogn) — 线性对数阶
- O(n^2) — 平方阶
O(1) — 常数阶
O(1) 的算法是一些运算次数为常数的算法。例如:
temp = a;
a = b;
b = temp;
根据守则: 用常数 1 来取代运行时间中所有加法常数。 上面语句共三条操作,单条操作的频度为 1,即使他有成千上万条操作,也只是个较大常数,这一类的时间复杂度为 O(1)。
O(N) — 线性阶
O(n) 的算法是一些线性算法。例如:
sum = 0;
for(i = 0; i < n; i++) {
sum++;
}
上面代码中第一行频度 1,第二行频度为 n,第三行频度为 1,所以 f(n)=n+n+1=2n+1。
根据守则: 只要高阶项,不要低阶项目,常数项置为 1,去除高阶项的系数: 所以时间复杂度 O(n)。这一类算法中操作次数和 n 正比线性增长。
O(log2N) — 对数阶
什么是对数? a^x = N,(a > 0 && a != 1),那么 x 即是以 a 为底,N 的对数,记作 其中 a 叫做对数的底数,N 叫做真数。
例 1:
private static void 对数阶() {
int number = 1; //执行1次
int n = 100; //执行1次
while (number < n) {
number = number * 2; //执行 n/2 次
System.out.println("哈哈"); //执行 1 次
}
}
假设 n 为 100,number 是 1,小于 100 退出循环。
- 第 1 次循环,number = 2,2^1。
- 第 2 次循环,number = 4, 2^2。
- 第 3 次循环,number = 8, 2^3。
- 第 x 次循环,number = 2^x
也就是 2^x=n 得出 x=log₂n。因此它的复杂度为 O(logn)。
例 2:
二分查找; 比如: 1,3,5,6,7,9;找出 7 如果全部遍历时间频度为 n; 二分查找每次砍断一半,即为 n/2; 随着查询次数的提升,频度变化作表:
| 查询次数 | 时间频度 |
|---|---|
| 1 | n/2 |
| 2 | n/2^2 |
| 3 | n/2^3 |
| k | n/2^k |
当最后找到 7 的时候时间频度则是 1; 也就是: n/2^k = 1; n = 2^k; k 则是以 2 为底,n 的对数,就是 Log2N; 那么二分查找的时间复杂度就是 O(Log2N)。
O(nlogn) — 线性对数阶
上面看了二分查找,是 LogN 的(LogN 没写底数默认就是 Log2N); 线性对数阶就是在 LogN 的基础上多了一个线性阶; 比如这么一个算法流程: 数组 a 和 b,a 的规模为 n,遍历的同时对 b 进行二分查找,如下代码:
for(int i = 0; i < n; i++)
binary_search(b);
}
O(n^2) — 平方阶
普通嵌套循环
private static void 普通平方阶() {
int n = 100;
for (int i = 0; i < n; i++) { //执行 n 次
for (int j = 0; j < n; j++) { //执行 n 次
System.out.println("哈哈");
}
}
}
这种就是 2 层循环嵌套起来,都是执行 n 次,属于乘方关系,它的时间复杂度为 O(n^2)。
等差数列嵌套循环
private static void 等差数列平方阶() {
int n = 100;
for (int i = 0; i < n; i++) { //执行 n 次
for (int j = i; j < n; j++) { //执行 n - i 次
System.out.println("哈哈");
}
}
}
基本式:
- i = 0,循环执行次数是 n 次。
- i = 1,循环执行次数是 n-1 次。
- i = 2,循环执行次数是 n-2 次。
- …
- i = n-1,循环执行的次数是 1 次。
换算式:
- result = n + (n - 1) + (n - 2) … + 1
- 被加数递减,抽象为一个等差数列求 n 项和的问题,公差为 1,带入公式,Sn = n(a1 + an ) ÷ 2
- result = (n(n+1))/2
- result = (n^2+n)/2
- result = (n^2)/2 + n/2
粗略计算时间复杂度的三部曲:
-
去掉运行时间中的所有加法常数。
-
只保留最高阶项。最高阶参考上面列出的按增长量级递增排列,于是只需要保留 result = (n^2)/2。
-
如果最高阶项存在且不是 1,去掉与这个最高阶相乘的常数得到时间复杂度。除以 2 相当于是乘以二分之一,去掉它,就得到,result = n^2,所以这个算法的时间复杂度为 O(n^2)。
时间复杂度的优劣对比
常见的数量级大小:越小表示算法的执行时间频度越短,则越优;
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)//2的n方<O(n!)<O(nn)//n的n方
参考
https://blog.csdn.net/user11223344abc/article/details/81485842